top of page

COMPLEX MODELS &

AUTHENTIC ASSESSMENT

As we learn about the different learning theories and approaches used by educators across the globe to help learners get the best learning experiences possible, the aspect of assessing/evaluating learners cannot be left untouched. Assessment is an important part of any learning experience as it gives both the learner and the teacher, a clear picture of the effectiveness of the lesson and the level of comprehension of the learner.

​

Although traditional assessment techniques such as multiple choice questions, subjective questions and essays can test a learner’s level of understanding of the concepts discussed in a lesson, they cannot bear witness to whether or not the learner is capable of applying these concepts in real-life scenarios.

​

This is where authentic assessments come in. Authentic assessments are tasks/activities learners engage in, to demonstrate their critical-thinking and problem-solving capabilities using concepts they have learnt in the classroom. Such assessments are often more interesting, engaging and rewarding for the learners. Some examples of such assessments are projects, portfolios, role-plays, creation of videos, etc.

​

Also related to effective pedagogy and learning are complex learning methods. Complex learning methods are approaches towards learning that center around the goal of learning being student-centered, and focus on strategies that can help make learning as long-lasting and effective for the learner as possible. Problem-based learning (PBL), experiential learning, service learning and gamification are some of the many complex learning methods used by instructors today.

​

See below for an example of a learning project developed using a complex learning method – gamification.

COMPLEX LEARNING PROJECT:

LET'S PLAY 'ALGEBRA'!!

LEARNING SCENARIO:

​

Overview:

For my project, I have chosen to create an activity-based lesson for a middle-school Algebra class. This is an example of a class I wish I could have been a part of, in place of my own middle-school learning experience in mathematics (click here to know more about it).

The lesson would take learners, step-by-step, through the concept of algebra, and help them learn how to solve numerical problems involving 2 as well as 3 variables.

​

Learning Objectives:

Learners will be able to:

  • Recognize the need to frame algebraic expressions

  • Solve numerical problems involving algebraic expressions containing 2 variables

  • Solve numerical problems involving algebraic expressions containing 3 variables

 

Learning Space:

This lesson plan has been created for a classroom activity. However, it may also be tweaked for a virtual classroom session.

 

Resources required:

A bunch of notecards/1 small whiteboard, 1 marker (1 set for each learner in class), 1 Desktop/Laptop computer, 1 Overhead projector/big screen TV (to project questions to the whole class), 1 large whiteboard with names of all learners listed in a table, as shown below.

URL of Game used for the Lesson: https://www.mathplayground.com/algebraic_reasoning.html

​

Lesson Plan:

  • As a pre-lesson activity/hook, project the game website for learners to see.

Image Source: Link

  • Start the first level of the game, and project the first question to the learners.

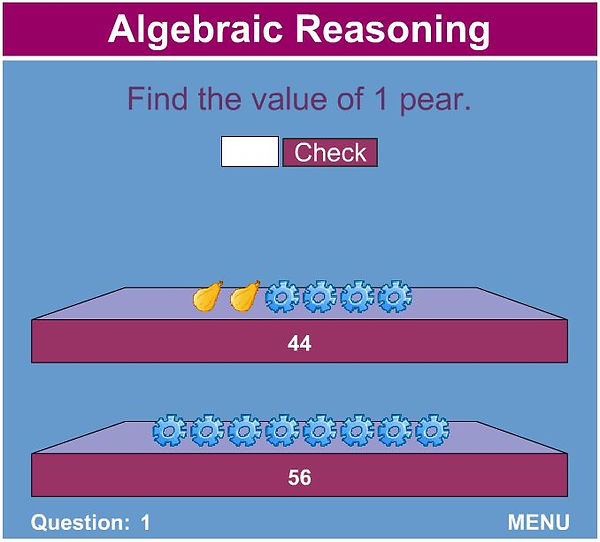
Image Source: Link

  • Ask learners to try to solve the problem on their own.

  • Give learners some time to solve the problem and walk around the class to identify ways in which learners might be trying to solve it.

  • Discuss learners’ answers/ways they tried to solve the problem.

  • Explain to learners that the problem can be solved in the following way.

 

We have two scenarios here:

4 wheels + 2 pears = 44

8 wheels = 56

This can be rephrased as:

(4 × Value of 1 wheel) + (2 × Value of 1 pear) = 44

(8 × Value of 1 wheel) = 56

First, we find the value of 1 wheel using the second scenario:

(8 × Value of 1 wheel) = 56

Hence, Value of 1 wheel = 56/8 = 8

Now, we use this value to find the value of 1 pear:

(4 × 8) + (2 × Value of 1 pear) = 44

32 + (2 × Value of 1 pear) = 44

(2 × Value of 1 pear) = 44 – 32

(2 × Value of 1 pear) = 12

Hence, Value of 1 pear = 12/2 = 6

  • Now, ask learners if it was easy to write ‘Value of 1 wheel’ and ‘Value of 1 pear’ during the whole calculation, or if they felt it was time consuming.

  • Using learners’ responses, introduce the concept of variables such as ‘x’ and ‘y’ to the class. Explain to learners, using the above example, why variables are used to solve problems.

  • Show learners how, using the variables, the ‘scenarios’ can be changed into algebraic equations:

Let Value of 1 wheel = x

      Value of 1 pear = y

Hence, the two scenarios turn into the following two equations:

4x + 2y = 44

8x = 56

  • Show learners how the same problem can now be solved in terms of x and y.

  • Now, start the game again and proceed from Level 1 Question 1.

  • Project each question to learners and ask them to solve it.

  • Instruct learners that, as they solve each question, they should write its answer in a notecard/on the small whiteboard, and hold it up so that you can see it.

  • As learners hold up their answers, note their answers in the respective box in the table drawn on the large whiteboard.

  • Once all learners share their answers, announce the correct answer and put a tick or a star-shaped sticker on their box in the table.

  • Progress with the rest of the game, and follow the above steps for each question. (In case the entire game is not finished in the first lesson, it can be continued in the next class.)

SCAFFOLDING

BADGING

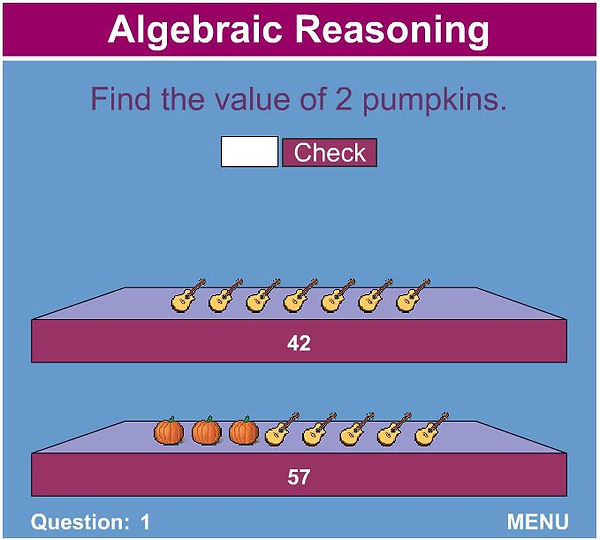
LEVEL 2

Image Source: Link

  • As you move up the levels of the game, provide appropriate scaffolding to learners, as required.

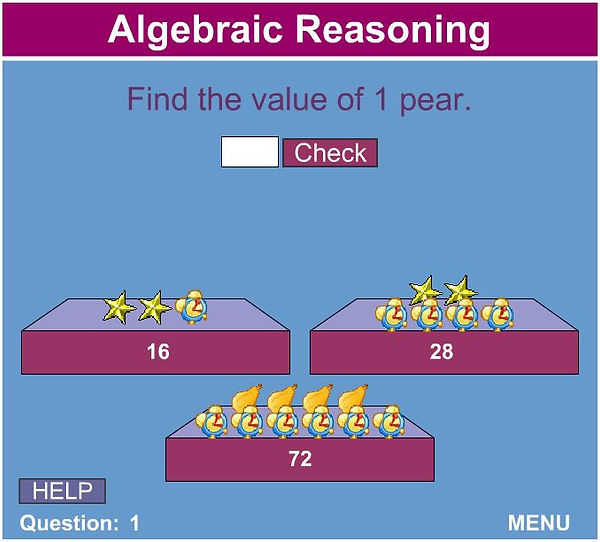
LEVEL 3

Image Source: Link

  • At the end of the lesson, announce the learners who solved the most questions correctly as WINNERS! Appreciate all learners for their progress, and encourage them to solve more such problems at home for practice.

​

COMPLEX LEARNING METHOD USED AND AUTHENTIC ASSESSMENT:

​

In the above described learning activity, the complex learning method used is Gamification. The activity assesses learners on the learning objectives listed, and also keeps the learners motivated and interested in the lesson throughout.

​

I think the assessment technique used here (solving numerical problems through a game) was authentic due to many reasons. Firstly, it had direct real-world relevance, as it involved solving numerical problems that can be easily tied to real-life scenarios. Secondly, it provided appropriate coaching and scaffolding. Lastly, the activity had an authentic context and resources.

 

Clearly, the activity relates to the ‘Gamification’ learning model as it uses two gaming techniques to pique the learners’ interest. The first is the use of the online game, and the second is the use of badging.

​

LEARNING THEORIES THAT BEST REPRESENT THIS DESIGN:

​

I think the primary learning theories involved in this activity are Cognitivism and Behaviorism. The cognitivist approach stems from the use of strategies and exercises that help learners comprehend the concept involved. The behaviorist approach lies in the use of positive reinforcement in the form of badging and appreciations that encourage learners to learn the topic.

References:

​

Note: 

  • Un-cited pictures, images and cliparts, if any, are either copyright-free or generated by the author herself.

bottom of page